RESP-M3 全般
FAQ一覧
- RESP-M3があれば、RESP-M/IIは不要なのですか?
- RESP-F3Dの機能を見ると、RESP-M3の特徴的な機能が全て網羅されており、F3DがあればM3は不要の気がするのですがどうですか?
- ねじれの単位は何ですか?
- ロッキングバネに関する重量(回転慣性重量モーメント)はどのように計算するのですか?
- 剛性マトリクス直接入力を行なうには、*STIFFコマンドでTKを指定するようですが、マトリクスファイルはどのように指定するのですか?
- フレームの数に上限があるのですか?
- 鉛直バネ(VS1コマンド)がありますが、上下動の解析が出来るのですか?
- 鉛直変位の等値指定は、どのような場合に用いるのですか?
- 解析結果の第1ステップは、どのような時刻なのですか?
- マルチシアスプリング(MSS)は、普通何本くらい設定するものなのですか?
- マルチシアスプリング(MSS)で非線形バネを使用する場合には、本数に応じて剛性・耐力を低減しなければならないのですか?
- マルチシアスプリング(MSS)で、LRB・高減衰ゴムのような複雑な復元力特性を使用する場合には、剛性・耐力低減係数をどこに指定すればよいのですか?
- RESP-F3の結果をQDMでモデル化したのですが、F3とM3の固有値を比較すると、ねじれのモードが一致しないのは、なぜですか?
- RESP-F2の結果をQDMでモデル化したのですが、ねじれのモードが得られないのは、なぜですか?
- 基礎免震の解析では、免震層として1層分取る方法、あるいは、スウェイのどちらでも扱えるようですが、どちらの方法がよいのですか?
- モード解析結果の一覧に、X・Y方向の刺激係数が示されますが、ねじれ(R)方向の刺激係数は出力されないのですか?
- 免震建物のねじれやすさは刺激関数図で検討できる、と訊いたのですが、なぜですか?
- 刺激関数図が、単位入力を受けたときの変形量を示すのであれば、変形量の単位は何ですか?
- 刺激関数図から判断した免震層のねじれやすさに比べて、応答解析の結果の方がねじれない傾向があるのはなぜですか?
- RESP-M3があれば、RESP-M/IIは不要なのですか?
-
RESP-M3は、ねじれ振動解析専用プログラムですので、原則的に1次元の串団子振動モデルを解くことはできません。
入力データを工夫することで、RESP-M3でもRESP-M/IIのような1次元解析を行うことは不可能ではありませんが、直交方向の応答を常に注意しながら作業を進める必要があり、作業性は極めて悪いと思われます。
- RESP-F3Dの機能を見ると、RESP-M3の特徴的な機能が全て網羅されており、F3DがあればM3は不要の気がするのですがどうですか?
-
RESP-M3が開発された当時は、計算機の能力が不足していたため、M3によるねじれ応答解析は非常に高価な解析だと考えられており、F3Dの立体解析に至っては将来技術だという認識が一般的でした。
しかし最近ではF3D解析でも比較的短時間で結果が得られるようになり、M3の利点が失われつつあるのが現状です。特にM3解析で必要なフレーム毎のスケルトンカーブのモデル化は煩雑な上に問題も多く、F3Dではこれらの作業が省略できる利点が評価されています。
作業量と計算時間のコストバランスにより、F3D解析が徐々に主流になっていくものと考えられます。
- ロッキングバネに関する重量(回転慣性重量モーメント)はどのように計算するのですか?
-
回転慣性重量モーメントは、(建物の重心からの距離の2乗)×(ある部分の重量)の計算を建物全体に積分して求めます。
RESP-M3は高さと水平距離の平面内で考えますので、ある点(x,y,z)の重量をmとした時には、原点に関する回転慣性重量モーメントは、X方向:m*(x*x+z*z)、Y方向:m*(y*y+z*z)と表すことが出来ます。
つまり、全ての節点重量に関して合計を計算すれば、原点に関する建物全体の回転慣性重量モーメントを求めることが出来ます。従って平面的な広がりに関する部分を、BASEコマンドで入力しなければならないことになります。
実際に値を求める手順としては、建物の支点反力図(地震重量による支点反力が望ましい)を用いて、全ての支点反力に対して建物重心からの距離の2乗をかけて合計を計算することが、一般的によく行われます。
RESP-M3利用者マニュアルのBASEコマンドの解説も参考にしてください。
- 剛性マトリクス直接入力を行なうには、*STIFFコマンドでTKを指定するようですが、マトリクスファイルはどのように指定するのですか?
-
パソコン版であれば、実行ウィンドウに「剛性マトリクスファイルを使う」というチェックボックスがありますので、これにチェックしてファイルのパスを入力してください。
Unix版であれば、run.m3.stifという実行スクリプトを利用することになります(run.m3.stif データ名 波形名 マトリクスファイル名)。
- 鉛直変位の等値指定は、どのような場合に用いるのですか?
-
塔状比が大きい建物や平面形状がL形の場合、X方向フレームと、Y方向のフレームの隅角部の鉛直変形を一致させないと、立体モデル(RESP-F3)と周期が一致しない場合があります(特にねじれモード)。
これは、直交フレームの拘束効果によるためですが、この拘束効果を考慮するための指定が、鉛直変位の等値指定になります。
内部的にこの指定は、幾何的な拘束条件を全体方程式に追加していますので、必要以上の指定は方程式の矛盾につながり、解が求まらなくなることがあります。全隅角点を指定する前に、対角の2点程度から指定されるのがよいと思われます。
- 解析結果の第1ステップは、どのような時刻なのですか?
-
入力波形の最初の数値の時刻が、積分刻みΔt秒としたときの第Δt秒となります。
第1ステップは、第0秒の解析結果ですので、RESP-M3では常に第1ステップの応答はゼロになります。
- マルチシアスプリング(MSS)は、普通何本くらい設定するものなのですか?
-
線形バネであれば、2本(X・Y各1本ずつ)で全方向に均等なバネが得られます。
非線形バネでは、通常6本、または、8本が採用されます。あまり細かくしても、計算時間がかかるだけで、計算精度にはほとんど影響ありません。
また、奇数本ではX・Y方向で対称にならないため、偶数本を指定するのがよいでしょう。
- マルチシアスプリング(MSS)で非線形バネを使用する場合には、本数に応じて剛性・耐力を低減しなければならないのですか?
-
剛性・耐力を別々に低減する必要があります。下表・下式に示す低減率を参考にしてください。最新バージョンからは、手作業による低減が不要な自動計算タイプが追加されていますので、そちらを利用されるほうが、手軽です。
本数 剛性低減係数 耐力低減係数 2 1.00000 1.00000 4 0.50000 0.41421 6 0.33333 0.26795 8 0.25000 0.19891 10 0.20000 0.15838 12 0.16667 0.13165 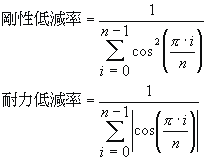
- マルチシアスプリング(MSS)で、LRB・高減衰ゴムのような複雑な復元力特性を使用する場合には、剛性・耐力低減係数をどこに指定すればよいのですか?
-
LRB系では、Kdに剛性低減率を、Qdに耐力低減率を掛けることになります。
高減衰積層ゴム系であれば、補正係数KGに剛性低減率を、補正係数KUに耐力低減率を指定することになります。ただし、これらの低減方法は、実験により確かめられた方法ではありませんし、メーカーの確認も取れておりません。
メーカーに問い合わせる前の参考と考えてください。
- RESP-F3の結果をQDMでモデル化したのですが、F3とM3の固有値を比較すると、ねじれのモードが一致しないのは、なぜですか?
-
ねじれ方向の回転慣性重量(INERTIAコマンド参照)が正しく入力されているか、単位は間違っていないかを確認する必要があります。データにまちがいが無いようであれば、鉛直変位の等値指定の項目も参考にして下さい。
- RESP-F2の結果をQDMでモデル化したのですが、ねじれのモードが得られないのは、なぜですか?
-
RESP-Fからの変換では、ねじれ方向の回転慣性重量を決定することが出来ませんので、ユーザ様がご自身で回転慣性重量を入力(INERTIAコマンド参照)する必要があります。入力時には、単位にも注意してください。
- 基礎免震の解析では、免震層として1層分取る方法、あるいは、スウェイのどちらでも扱えるようですが、どちらの方法が良いのですか?
-
スウェイを免震層として入力してください。
1階を免震層として入力する方法もありますが、上部構造に剛性比例減衰を与えるために、免震層をロックした場合の固有値を採用する必要がありますが、一般階を免震とするとロックが自由に行なえません。
- モード解析結果の一覧に、X・Y方向の刺激係数が示されますが、ねじれ(R)方向の刺激係数は出力されないのですか?
-
刺激係数は、モード毎にある方向の単位入力を受けた場合の変形量の最大値を示します。
M3には、X・Y・ねじれの各自由度がありますので、それぞれの方向から単位入力を受けた場合の最大変形量が算出できることになります。ただし、ねじれ方向の地震入力は通常無いものと考えられますので、X・Yの2方向から単位入力を対象としています。
- 免震建物のねじれやすさは刺激関数図で検討できる、と訊いたのですが、なぜですか?
-
建物のねじれを決定する要因として、剛性と重量のバランス、および、地震入力が挙げられます。
剛性と重量のバランスは、偏心率でねじれやすさを知ることが出来、モード解析することで、地震入力を受けた場合にねじれのモードが卓越しているかどうかを知ることが出来ます。
しかし実際には、地震を受けてねじれますので、単位入力に対するねじれ変形量で評価する方法が直接的といえます。刺激関数図は、ある方向に単位入力を受けた場合の変形量を示しますので、ねじれ量の直接的な予測が出来ます。
- 刺激関数図が、単位入力を受けたときの変形量を示すのであれば、変形量の単位は何ですか?
-
任意位置の刺激関数を求める方法を下式に示します。式の意味としては、「当該モードに相当する1質点系の応答変位が1」となるような入力を受けたときの応答変位になりますので、刺激関数は無次元量です。
- X入力時刺激関数xi = (βxi・Vxi・qi + L・cos(R+βxi・Vri・qi) ? X) / qi
- X入力時刺激関数yi = (βxi・Vyi・qi + L・sin(R+βxi・Vri・qi) ? Y) / qi
- Y入力時刺激関数xi = (βyi・Vxi・qi + L・cos(R+βyi・Vri・qi) ? X) / qi
- Y入力時刺激関数yi = (βyi・Vyi・qi + L・sin(R+βyi・Vri・qi) ? Y) / qi
添字i 第i次のモード 添字x x方向成分 添字y y方向成分 添字r ねじれ方向成分 L 重心から当該地点までの直線距離 X 重心を原点とした時の当該地点のX座標 R 重心を原点とした時の当該地点の角度 β 刺激係数 V 固有ベクトル q 当該モードしか存在しない系の応答変位(1として考える)
- 刺激関数図から判断した免震層のねじれやすさに比べて、応答解析の結果の方がねじれない傾向があるのはなぜですか?
-
非線形の免震装置(LRB,高減衰ゴムなど)の場合、マルチシアスプリング(MSS)の理論に従えば、加振方向の剛性低下に比べ、直交方向の剛性低下は小さくなります。
このため、一旦ある方向に変形が進むと、変形方向に剛性が低下し、さらにその方向に変形しやすくなりますが、直交方向にはあまり剛性低下せず変形は進みません。
しかし、一般にモード解析では、全方向に均等に剛性低下させた免震装置を仮定します。このような解析条件の違いのために、多くの場合、非線形時刻歴応答解析の方がねじれにくい結果となります。